97 x 93 im Kopf ausrechnen? Bei einigen Aufgaben, die ihr auf diesen Seiten seht, werdet ihr erst einmal denken: Das schaffen doch höchstens Genies! Irrtum. Die haben sich nämlich Wege ausgedacht, mit denen jeder solche Kopfnüsse knacken kann. Im zweiten Teil unserer Serie zeigen wir euch einige der raffiniertesten Rechenmethoden.
Rechnen mit den Fingern
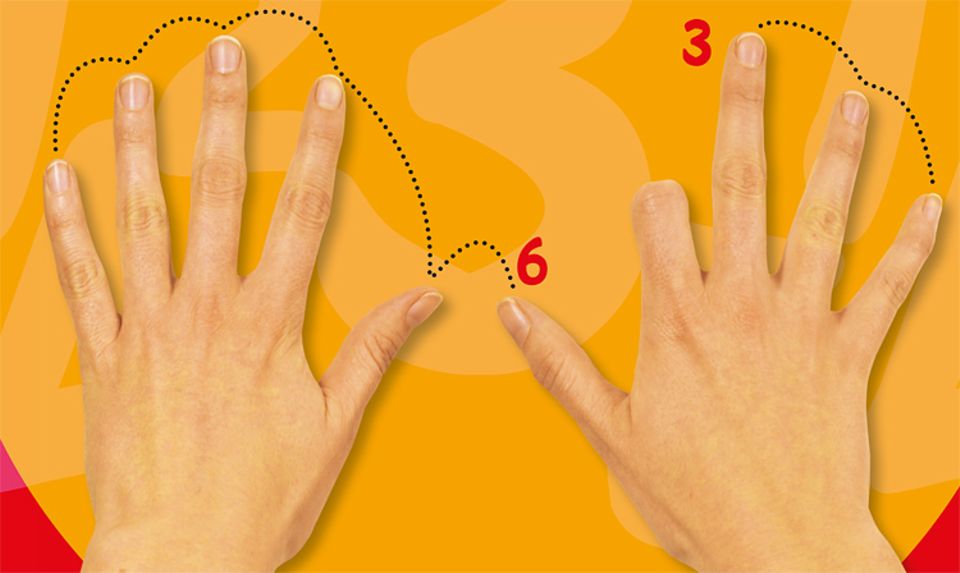
Zum Einstieg ein einfacher Trick, mit dem ihr einstellige Zahlen mit 9 multiplizieren könnt. Wir zeigen es euch am Beispiel 7 x 9
Wie geht's?
Haltet einfach die beiden Hände mit gespreizten Fingern vor euch. Nun zählt von links nach rechts bis zum siebten Finger und knickt ihn um. Links von ihm sind nun sechs Finger stehen geblieben. Das sind die Zehner. Rechts vom umgeknickten Finger habt ihr die Einer. Das Ergebnis ist also: 60 + 3 = 63!
Blitzschnell Multiplizieren mit 5
Manchmal ist es besser, eine schwere Rechnung durch zwei leichte zu ersetzen. Das zeigt diese Methode, mit der ihr Zahlen mit 5 multiplizieren könnt. Beispiel: 84 x 5
Wie geht's?
5 ist nichts anderes als ½ × 10. Statt 84 × 5 könnt ihr deshalb auch rechnen: 84 × ½ × 10. Anders geschrieben: 84 : 2 × 10 Machen wir das der Reihe nach:
Erster Schritt: 84 : 2 = 42
Zweiter Schritt: Das Ergebnis mit 10 multiplizieren - also einfach eine 0 anhängen: 42 × 10 = 420
Natürlich klappt der Trick auch mit ungeraden Zahlen. Sehen wir uns 65 × 5 an! Beim ersten Schritt steht zwar ein Komma im Ergebnis (... igitt ): 65 : 2 = 32,5 Doch das verschwindet sofort im zweiten. Denn mit 10 zu multiplizieren heißt ja nur, das Komma eine Stelle nach rechts zu schieben: 32,5 × 10 = 325
Grosse Zahlen? Klein machen!
Der folgende Trick ist eine Fortführung des vorangegangenen und funktioniert für große Zahlen, die man in mehrere Päckchen aus geraden Zahlen zerlegen kann. Sehen wir uns das an der Zahl 4 418 296 an. Beispiel: 4 418 296 × 5
Wie geht's?
Erster Schritt: Teilt 4 418 296 in kleine Blöcke: 44 / 18 / 296
Zweiter Schritt: Nun fahrt fort ihr wie im vorherigen Trick. Teilt also erst durch 2. Passt dabei auf, dass in jedem Block die Anzahl der Ziffern gleich bleibt: 22 / 09 / 148
Dritter Schritt: Setzt sie wieder zusammen und multipliziert mit 10 (also hängt eine 0 an). Schon steht das Ergebnis da: 22 091 480
Rechnen wie Gauss
Carl Friedrich Gauß (1777–1855) war ein genialer Mathematiker. Folgenden Trick hat er angeblich entdeckt, als er erst sieben Jahre alt war! Damals fragte ihn sein Mathelehrer (um ihn zu ärgern), was herauskommt, wenn man alle Zahlen von 1 bis 100 zusammenzählt. Gauß überlegte einen Moment und gab die korrekte Antwort: 5050.
Wie geht's?
Stellt euch vor, ihr schreibt alle Zahlen nebeneinander auf. Also links die 1, dann die 2, die 3 … bis ganz rechts die 100. Was kommt heraus, wenn ihr die erste (1) und die letzte (100) Zahl zusammenzählt? Klar: 101. Nun rechnet die zweite und die zweitletzte Zahl zusammen, und dritte und die drittletzte und so fort:
2 + 99
3 + 98
...

Jedes Mal ist das Ergebnis 101! Insgesamt bekommt ihr 50 Paare, oder anders geschrieben:
50 × 101 =
50 × 100 + 50 × 1 = 5000 + 50 =
5050
Vedisch Multiplizieren
Diese Methode ist nach alten indischen Schriften, den Veden, benannt. Fest steht: Man kann damit rasend schnell Zahlen multiplizieren, die beide knapp unter 100 oder 1000 liegen. Beispiel: 98 × 93
Wie geht's
Erster Schritt: Schreibt die Zahlen nebeneinander.
98 93
Zweiter Schritt: Rechnet die jeweilige Differenz zu 100 aus und schreibt die Zahlen in die Zeile darunter.
98 93
2 7
Dritter Schritt: Zieht eine der unteren Zahlen von der ab, die schräg darüber steht (ob die linke von der rechten oder umgekehrt, ist egal):
93– 2 = 91
Vierter Schritt: Schreibt die gleiche Zahl an Nullen dahinter:
9100
Fünfter Schritt: Jetzt multipliziert die unteren beiden.
2 × 7 = 14
Sechster Schritt: Addiert die Zahlen (also 9100 und 14), und ihr bekommt das Ergebnis: 9114

Der Kniff des Rechenkünstlers
Der Mathematiker Jakow Trachtenberg (1888–1953) hat gleich eine ganze Reihe toller Rechentricks ausgeknobelt. Das Besondere daran: Trachtenberg multiplizierte, indem er Zahlen zusammenzählte. Viele der schnellsten Kopfrechner der Welt benutzen heute Trachtenbergs System. Schauen wir uns an, wie er mit 11 multipliziert. Beispiel: 72 × 11
Wie geht's
Zieht die erste und die zweite Zahl auseinander...
7 2
... und schreibt in die Mitte die Summe der beiden. Schon habt ihr das Ergebnis:
7 / 7 + 2 / 2 = 792
Wow! Der Trick klappt auch mit größeren Zahlen. Ihr müsst nur jede Ziffer mit ihrem Nachbarn addieren und das Ergebnis in die Mitte eintragen:
536 × 11 = 5 / 5 + 3 / 3 + 6 / 6 = 5896
Achtung: Wenn eine Summe größer als 9 wird, addiert die 1 zur Zahl links davon, also:
83 × 11 = 8 / 8 + 3 / 3 oder 8 / 11 / 3 = 913
Für Spezialisten
Manche Rechentricks funktionieren nur in Spezialfällen. Mit diesem hier lassen sich schnell zweistellige Zahlen multiplizieren, wenn ihre ersten Stellen (die Zehner) gleich sind und die letzten Stellen (die Einer) zusammen 10 ergeben. Beispiel: 97 × 93
Kleiner Check: 7 + 3 = 10. Okay!
Wie geht's?
Multipliziert die Zehnerstellen miteinander und macht dabei die erste um 1 größer:
10 × 9 = 90
Nun multipliziert die Einer:
3 × 7 = 21
und setzt beide Zahlen zusammen. Schon habt ihr das Ergebnis: 9021
Achtung: Bekommt ihr bei den Einern ein einstelliges Ergebnis, setzt eine 0 davor:
91 × 99 = 9009
Der Kniff funktioniert auch bei dreistelligen Zahlen: Beispiel: 135 x 135
14 x 13 = 182 und 5 x 5 = 25
Das ergibt: 18225
Chinesisch Multiplizieren
Dieser Kniff stammt angeblich aus China. Mit ihm lassen sich leicht zwei- oder dreistellige Zahlen multiplizieren. Und zwar, ohne eine einzige Multiplikation zu machen! Beispiel: 32 × 21
Wie geht's?

Erster Schritt:Zeichnet für jede der Ziffern so viele Linien auf ein Blatt Papier, wie ihrem Wert entspricht. Die Linien der ersten Zahl laufen dabei von links unten nach rechts oben. Also: Ihr zieht drei Linien für die erste Ziffer (die 3), lasst eine kleine Lücke und zeichnet darunter noch zwei Linien (für die 2).

Zweiter Schritt: Die Linien der zweiten Zahl zieht ihr von links oben nach rechts unten. Wichtig: Diesmal liegen die Linien der ersten Ziffer unterhalb der zweiten: zwei Linien (für die 2), eine Lücke, darüber eine Linie (für die 1).
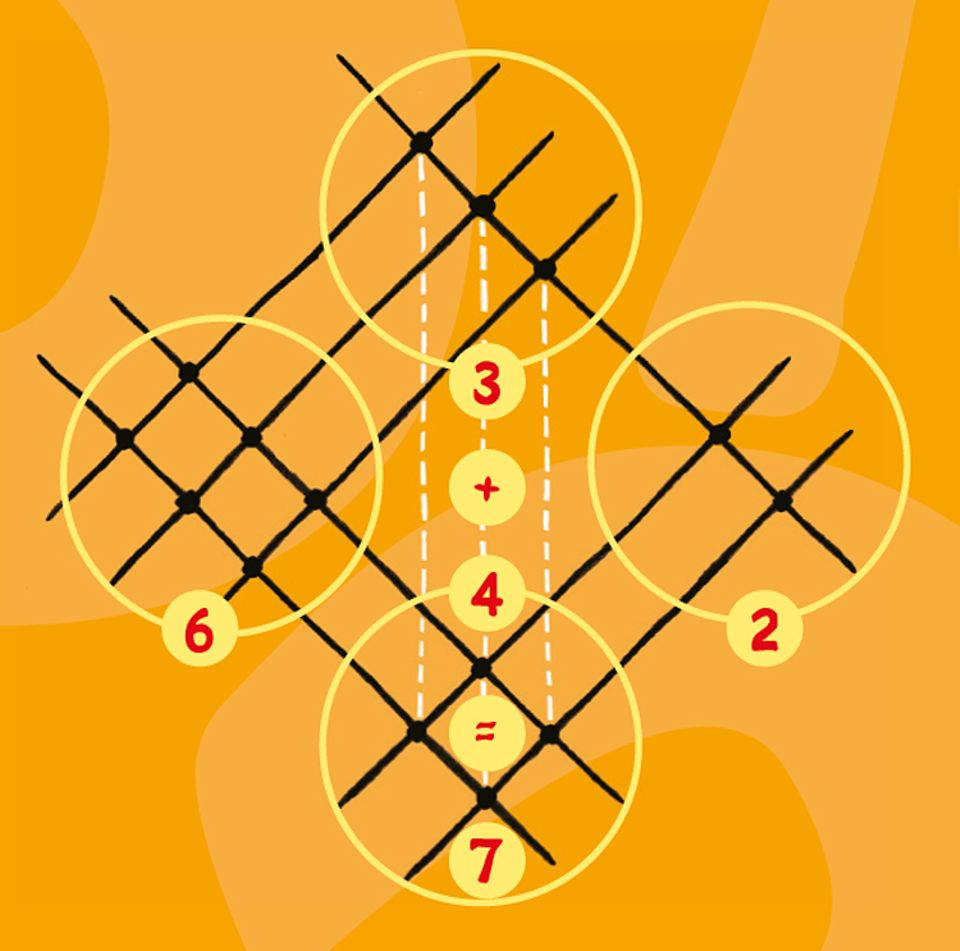
Dritter Schritt: Nun ist das Bild fertig. Jetzt müsst ihr nur noch die Schnittstellen auszählen, die übereinanderliegen. Und zwar von links nach rechts: 672.
Achtung: Manchmal wird eine Schnittstellenzahl zweistellig. Dann addiert einfach die erste Ziffer zur Zahl links davon. Bei 52 × 12 etwa habt ihr 5, 12 und 4 Schnittstellen. Das Ergebnis ist dann: (5 + 1) 2 4 = 624
Tipp:
Dieser Trick funktioniert besser bei kleinen Ziffern. Bei großen müsst ihr zu viele Schnittstellen zählen.
Sag mir, ob du teilbar bist!
Mit folgenden Methoden könnt ihr in wenigen Momenten sehen, ob eine beliebige Zahl durch 3 oder 11 teilbar ist. Beispiel: 104 973
Wie geht's?
Ob die Zahl durch 3 teilbar ist, erkennt ihr fix: Schaut einfach, ob die Quersumme der Zahl durch 3 teilbar ist. Was war gleich die Quersumme? Ach, ja: Die Summe aller Ziffern der Zahl - bei 12 wäre das zum Beispiel 1 + 2 = 3. Also:
Quersumme von 104 973 = 1 + 0 + 4 + 9 + 7 + 3 = 24
Ist 24 durch 3 teilbar? Klar (das ergibt 8). Also ist es auch 104 973. (Das Ergebnis ist 34 991.) Verblüffend, oder?
Ganz ähnlich könnt ihr schauen, ob eine Zahl durch 11 teilbar ist. Ihr müsst nur statt der Quersumme die „alternierende Quersumme“ ausrechnen. Die bekommt ihr, wenn ihr die Zahlen abwechselnd abzieht und hinzuzählt. Also:
1 – 0 + 4 – 9 + 7 – 3 = 0
Glück gehabt: Auch 0 geteilt durch 11 ergibt eine ganze Zahl – nämlich einfach wieder 0. Also ist 104 973 auch durch 11 teilbar (das Ergebnis ist 9543)!
Zahlen Merken
Viele Zahlenakrobaten können nicht nur blitzschnell rechnen. Manche können sich auch unglaubliche Mengen an Zahlen merken. Zum Teil über 1000 in einer halben Stunde. Wir fangen besser klein an. Beispiel: 8456
Wie geht's?
Das menschliche Gehirn merkt sich nicht gern Zahlen, aber umso lieber Bilder und Geschichten. Ein Trick von Gedächtniskünstlern ist deshalb, Zahlen in Bilder zu übersetzen und daraus eine Geschichte zu machen. Bilder von 0 bis 9:
0 = Ball
1 = Kerze
2 = Schwan
3 = Dreizack
4 = Stuhl
5 = Hand
6 = Würfel
7= Zwerg
8 = Schneemann
9 = Tennisschläger
Wie merkt man sich nun 8456? Zum Beispiel so: Ein Schneemann setzt sich auf einen Stuhl und wirft mit seiner Hand einen Würfel.
Jetzt seid ihr dran!
Seht ihr? Man muss kein Genie sein um kniffelige Aufgaben zu lösen, wenn man die richtigen Lösungswege kennt. Versucht es doch einmal selbst.